Bangun Ruang: Pengertian, Jenis, Rumus, Contoh Soal

 Pembahasan pada artikel kali ini yaitu mengenai bangun ruang.

Tentu kalian sudah mengetahui mengenai bangun ruang. Bangun ruang merupakan salah satu materi matematika yang dikelompokkan dalam topik geometri.

Banyak sekali bentuk bangu ruang. Terdapat bangun ruang dengan bentuk beraturan dan tak-beraturan.

Untuk lebih memahami mengenai bangun ruang perhatikan penjelasan berikut ini.

Pengertian Bangun Ruang

Apa yang kamu ketahui mengenai bangun ruang?

Bangun ruang merupakan salah satu objek matematika yang mempelajari mengenai bangun tiga dimensi.

Seperti apakah bangun tiga dimensi tersebut?

Bangun tiga dimensi merupakan bangun yang memiliki volume (isi). Bangun ruang memiliki beraneka ragam bentuk serta banyak diterapkan dalam kehidupan sehari-hari.

Bangun Ruang dalam Kehidupan Sehari-Hari

Bangun ruang memiliki beberapa penerapan dalam kehidupan sehari-hari.

Beberapa contoh penerapan bangun ruang dapat kita lihat pada benda-benda yang menyerupai bentuk bangun ruang, misalnya:

• bentuk lemari menyerupai bangun balok
• bentuk dadu menyerupai bangun kubus
• bentuk kaleng menyerupai bangun tabung
• bentuk piramida menyerupai bentuk limas
• bentuk kelereng menyerupai bentuk bola
• bentuk terompet menyerupai bantuk kerucut
• dan sebagainya.

Macam-Macam Bangun Ruang

Bangun ruang memiliki beberapa macam. Berdasarka bentuknya, bangun ruang dibagi menjadi dua, yaitu bangun ruang sisi datar dan bangun ruang sisi lengkung.

Bangun ruang sisi datar meliputi, kubus, balok, prisma, dan limas. Bangun ruang sisi lengkung meliputi, tabung, kerucut, dan bola.

Bangun Ruang Sisi Datar

Telah disebutkan pada bagian sebelumnya bahwa bangun ruang sisi datar terdiri dari kubus, balok, prisma, dan limas. Pembahasan mengenai bangun ruang sisi datar akan dijelaskan pada bagian ini.

1. Kubus

Perhatikan gambar di bawah ini.

Bangun ruang di atas adalah kubus. Kubus merupakan bangun ruang sisi datar yang memiliki 6 sisi yang berbentuk persegi.

Bangun kubus memiliki 12 rusuk yang sama panjang. Diagonal ruang kubus ada 4 dan bidang diagonal kubus ada 6.

Baca Selengkapnya di Kubus

2. Balok

Perhatikan gambar berikut.

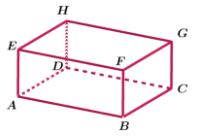
Pada gambar tersebut terdapat balok yang terdiri dari 6 sisi. Bangun balok memiliki 12 rusuk, 4 diagonal ruang, dan 6 bidang diagonal.

3. Prisma

Perhatikan bangun limas berikut.

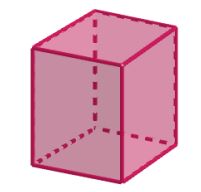
Bangun prisma merupakan bangun ruang yang memiliki alas dan tutup. Alas dan tutup prisma merupakan dua bangun segibanyak yang kongruen. Balok dan kubus termasuk dalam prisma dengan alas dan tutup berbentuk segiempat.

4. Limas

Perhatikan gambar berikut.

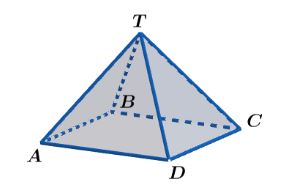
Pada gambar di atas terdapat limas dengan puncak titik T. Limas hanya memiliki alas dengan bentuk segibanyak. Limas segi-n memiliki n + 1 sisi dan 2n rusuk.

Bangun Ruang Sisi Lengkung

Beberapa bentuk bangun ruang sisi lengkung yaitu tabung, kerucut, dan bola. Perhatikan penjelasan di bawah ini.

1. Tabung

Perhatikan gambar berikut.

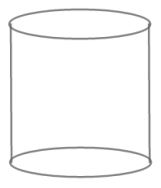
Pada gambar di atas terdapat bangun tabung. Tabung memiliki 3 sisi dengan alas dan tutup berupa lingkaran.

2. Kerucut

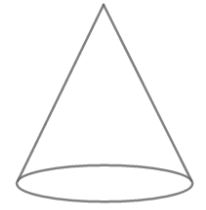
Bangun di atas merupakan bangun kerucut dengan alas berupa lingkaran. Kerucut mempunyai dua sisi yaitu sisi alas lingkaran berupa lingkaran dan selimut kerucut.

Baca Selengkapnya di Kerucut

3. Bola

Perhatikan gambar berikut.

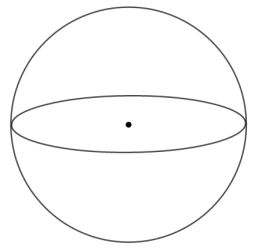
Pada gambar di atas terdapat bangun bola. Bangun bola memiliki 1 sisi. Dalam bangun bola, setiap titik pada permukaan bola memiliki jarak yang sama dengan titik pusat bola yang disebut dengan jari-jari bola.

Jaring-Jaring Bangun Ruang

Pada bagian ini, akan disajikan beberapa contoh jaring-jaring bangun ruang diantaranya jaring-jaring kubus, balok, prisma, limas, tabung, dan kerucut.

1. Jaring-jaring kubus

Berikut merupakan jaring-jaring kubus.

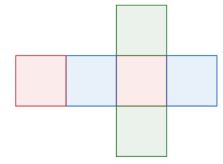
2. Jaring-jaring balok

Berikut merupakan jaring-jaring balok.

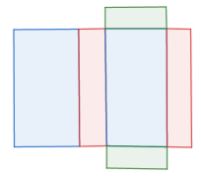
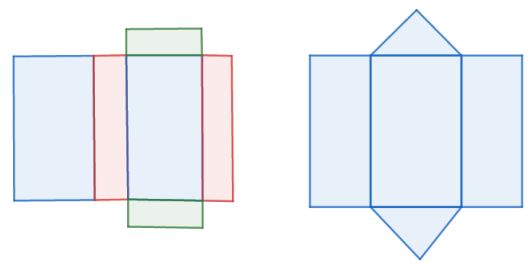
3. Jaring-jaring prisma

Berikut merupakan jaring-jaring prisma segitiga dan prisma segiempat.

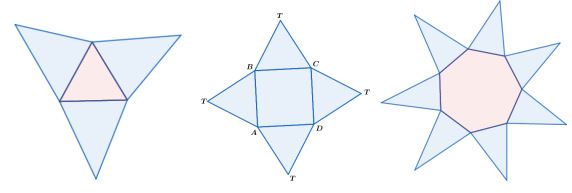
4. Jaring-jaring limas

Berikut merupakan beberapa jaring-jaring limas.

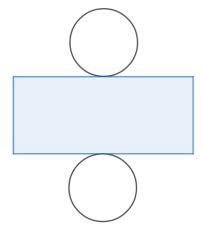
5. Jaring-jaring tabung

Berikut merupakan jaring-jaring tabung

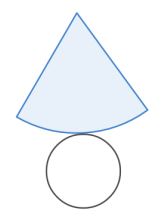
6. Jaring-jaring kerucut

Berikut merupakan jaring-jaring kerucut.

Perhatikan penjelasan di bawah ini mengenai rumus bangun ruang.

Rumus Volume Bangun Ruang

Pambahasan mengenai rumus bangun ruang pada bagian ini yaitu mengenai rumus volume bangun ruang.

Berikut merupakan rumus volume bangun ruang.

Bangun Ruang	Rumus Volume
Kubus	V = r x r x r Keterangan r  : ukuran rusuk kubus
Balok	V =  p x l x t Keterangan p  : ukuran panjang balok l   : ukuran lebar balok t   : ukuran tinggi balok
Prisma	V = Luas alas x tinggi
Limas	V = 1/3 x Luas alas x tinggi
Tabung	V = π x r x r x t Keterangan π  : konstanta (3,14 atau 22/7) r   : ukuran jari-jari alas t   : ukuran tinggi tabung
Kerucut	V = 1/3 x π x r x r x t Keterangan π  : konstanta (3,14 atau 22/7) r   : ukuran jari-jari alas t   : ukuran tinggi kerucut
Bola	V = 4/3 x π x r x r x r Keterangan π  : konstanta (3,14 atau 22/7) r   : ukuran jari-jari bola

Kerjakan soal berikut untuk meningkatkan pemahaman kalian mengenai bangun ruang.

Contoh Soal Bangun Ruang

1. Sebuah balok berukuran panjang 12 cm, lebar 9 cm, dan tinggi 5 cm. Volume balok tersebut adalah . . . .

Pembahasan

V = p x l x t

V = 12 cm x 9 cm x 5 cm

V = 540 cm3

2. Suatu kubus memiliki ukuran rusuk 12 cm. Volume kubus tersebut adalah . . . .

Pembahasan

V = r x r x r

V = 12 cm x 12 cm x 12 cm

V = 1.728 cm3

3. Sebuah kerucut dimasukkan ke dalam tabung sehingga puncak kerucut menyinggung tutup tabung. Jika ukuran alas kerucut dan tabung sama. Tentukan perbandingan volume kerucut dengan volume tabung.

Pembahasan

V kerucut/V tabung = (1/3 x π x r x r x t)/( π x r x r x t) = 1/3

Jadi, perbandingan volume kerucut dengan volume tabung adalah 1 : 3.

4. Suatu bola memiliki ukuran jari-jari 3 cm. Jika ukuran jari-jari diperbesar menjadi dua kali jari-jari semula, maka berapa kali volume bola sekarang dari volume bola sebelum diperbesar?

Pembahasan

V awal = 4/3 x π x 3 x 3 x 3 = 36 π

V akhir = 4/3 x π x 6 x 6 x 6 = 288 π

Volume akhir merupakan 8 kali volum bola mula-mula (sebelum diperbesar).